Lista de probleme 1033

Subprogramul consecutiv are doi parametri:

• n, prin care primește un număr natural (n∈[1,104]);
• f , prin care furnizează un număr natural cu proprietatea: (f-1)∙f < n ≤ f∙(f+1).

Scrieți definiția completă a subprogramului C++.

Numărul natural an este ascendent al numărului natural n, dacă oricare dintre cifrele lui an este mai mare sau egală cu cifra unităților lui n.

Exemplu: oricare dintre numerele 7, 9, 98 sau 7998 este ascendent al lui 827, dar numărul 857 nu este ascendent al lui 827.

Subprogramul ascendent are trei parametri:

• n, prin care primește un număr natural (n∈[0,1000));
• x și y, prin care primește câte un număr natural din intervalul [0,1000) (x<y).

Subprogramul returnează suma ascendenților lui n din intervalul [x,y], sau valoarea 0, dacă nu există niciun astfel de ascendent. Scrieți definiția completă a subprogramului C++.

Un cuvânt semioglindit se obţine dintr-un cuvânt cu 2·k (k∈[1,100]) litere, prin interschimbarea în acesta a secvenței formate din primele k litere cu secvența formată din ultimele k litere.

Exemplu: din cuvântul platim se obţine cuvântul semioglindit timpla.

Într-un text de cel mult 200 de caractere, cuvintele sunt formate din litere mici ale alfabetului englez și sunt separate prin câte un spaţiu. Scrieţi un program care citeşte de la tastatură un text de tipul precizat, pe care îl transformă în memorie, prin înlocuirea fiecărui cuvânt cu număr par de litere, cu cel semioglindit obținut din acesta. Programul afișează pe ecran textul obținut, sau mesajul nu exista, dacă toate cuvintele au număr impar de litere.

În urma petrecerii de ziua lui RAU-Gigel, copiii au primit atâtea bomboane încât au câștigat o energie debordantă – așa că l-au provocat pe RAU-Gigel la un concurs de … numărat!

Acestora li se dă o matrice cu N linii și M coloane, în care fiecare element este un număr natural nenul. Obiectivul lor este să determine câte submatrice (sub-dreptunghiuri formate din linii și coloane contigue) conțin exact K valori distincte.

RAU-Gigel își serbează ziua alături de colegii săi de la clubul de informatică și vrea să le împartă bomboane. El are un număr dat de bomboane și ar vrea să știe dacă îi ajung și, dacă da, în câte moduri le poate împărți. Dar nu își amintește câți colegi are la cerc, are însă o informație care ar putea să îl ajute.

Pentru a îmbunătăţi aptitudinile logico-matematice ale elevilor săi, profesorul Vasile a implementat un joc. Pe ecranul principal al jocului se afişează un şir de N scaune, numerotate de la stânga spre dreapta începând cu 1, pe fiecare scaun fiind așezat câte un copil. Fiecare copil poartă un tricou pe care este scris, de asemenea, câte un număr de la 1 la N. Numerele de pe tricouri sunt distincte și sunt scrise pe spate, deci nu sunt vizibile. Scopul jocului este de a descoperi numărul scris pe tricoul fiecărui copil. Pentru aceasta, pe ecran mai este afişat un triunghi de numere T, care ne dă informaţii ajutătoare. Triunghiul arată ca o matrice în care liniile sunt numerotate de sus în jos de la 1 la N, iar coloanele de la stânga la dreapta de la 1 la N. Numărul scris în triunghi pe linia i şi coloana j (1 ≤ i ≤ j ≤ n) reprezintă numărul scaunului pe care stă copilul având cel mai mic număr pe tricou dintre toţi copiii situaţi pe scaune cu numere cuprinse între i şi j (inclusiv i şi j). Observaţi că poziţiile din triunghi de pe linia i şi coloana j cu 1 ≤ j < i ≤ N nu sunt completate. Cunoscând numărul de copii şi triunghiul de numere:
1. determinați o soluţie posibilă; dacă există mai multe soluţii posibile se va afişa cea mai mică din punctul de vedere lexicografic;
2. determinați numărul de soluţii posibile.

Alina, managerul unui lanț de magazine, este responsabilă de gestiunea tranzacțiilor bancare din cadrul acestora. Ea lucrează cu conturi bancare și cunoaște sumele de bani (soldul) existente în fiecare dintre acestea. Se cunosc N, numărul tranzacțiilor și N numere întregi nenule a[1], a[2], …, a[N], reprezentând, în această ordine, sumele de tranzacționat (un număr pozitiv indică o sumă care urmează a fi depusă, iar un număr negativ reprezintă o sumă care urmează a fi retrasă). După procesarea celor N tranzacții, ajutați-o pe Alina să determine:
1) numărul de conturi rămase active.
2) soldul maxim care se găsește într-un cont dintre cele rămase active.

Se dau Q query-uri de forma n k. Pentru fiecare query să se afișeze numărul de partiții ale unei mulțimi cu n elemente în n/k submulțimi neordonate cu câte k elemente.

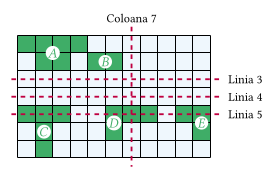
Privit din satelit, Golful Biscayne (Florida) este format din n × m celule pătratice, fiecare celulă fiind umplută fie cu pământ, fie cu apă. Celulele umplute cu pământ sunt grupate în insule: două celule umplute cu pământ fac parte din aceeași insulă dacă și numai dacă se poate ajunge de la una la cealaltă prin deplasare (în sus, jos, stânga sau dreapta) doar pe pământ.

Golful poate fi văzut, astfel, ca o matrice A cu n linii și m coloane (numerotate de la 1), unde A[i][j] = 1 dacă celula de pe linia i și coloana j este umplută cu pământ și A[i][j] = 0 dacă este umplută cu apă.

Spunem că o insulă se află la stânga unei coloane c dacă și numai dacă toate celulele ce intră în alcătuirea insulei sunt strict la stânga coloanei c, adică sunt situate pe coloane strict mai mici decât c. Analog, stabilim dacă o insulă se află la dreapta unei coloane c, respectiv deasupra sau dedesubtul unei linii l. De exemplu, în desenul de mai sus, insulele A, B și C sunt la stânga coloanei 7, insula E este la dreapta coloanei 7, iar insula D nu este nici la stânga, nici la dreapta coloanei 7. De asemenea, insulele A și B sunt deasupra liniei 3, iar insulele C, D și E sunt dedesubtul liniei 4. Mai mult, insulele C, D și E nu sunt nici deasupra, nici dedesubtul liniei 5.

Problema are trei cerințe, cerința de rezolvat fiind dată de T ∈ {1, 2, 3}.

• T = 1. Determinați numărul de celule din golf ce sunt umplute cu pământ.
• T = 2. Determinați numărul de insule din golf ce conțin un număr maxim de celule. Dacă nu există nicio insulă, atunci valoarea acestui număr este 0.
• T = 3. Se dau, în ordine, Q interogări, fiecare fiind descrisă printr-o literă și un număr natural
  nenul p. Determinați valoarea produsului a × b, știind că:
  • Dacă litera este C, atunci a reprezintă numărul de celule din toate insulele ce se află la stânga coloanei p (1 ≤ p ≤ m) și b numărul de celule din toate insulele ce se află la dreapta coloanei p.
  • Dacă litera este L, atunci a reprezintă numărul de celule din toate insulele ce se află deasupra liniei p (1 ≤ p ≤ n) și b numărul de celule din toate insulele ce se află dedesubtul liniei p.

Fie a = (a[1], a[2], ..., a[n]) un șir de n numere întregi. Pentru fiecare k ∈ {1,2, ...,n}, definim min[k] = min{a[1], a[2], ... ,a[k]} și max[k] = max{a[1], a[2], ...,a[k]}. Astfel, asociem șirului a un alt șir de intervale închise minmax = ([min[1], max[1]], [min[2], max[2]], ..., [min[n], max[n]]). Vom spune că șirul a este un șir cromatic dacă și numai dacă elementele șirului minmax sunt distincte două câte două, adică nu există două intervale identice în șir. Dându-se un șir a, nu neapărat cromatic, să se determine:

• Numărul de șiruri cromatice NSC ce se pot forma prin rearanjarea elementelor șirului a. Întrucât acest număr poate fi foarte mare, se cere NSC modulo 1.000.000.007.
• Știind că șirul a este cromatic, să se determine poziția p ∈ {1, 2, ..., NSC} a șirului a în lista ordonată lexicografic a tuturor permutărilor cromatice ale lui a.
• Dat fiind q ∈ {1, 2, ..., NSC}, să se determine cel de-al q-lea șir cromatic în ordine lexicografică ce se poate obține prin rearanjarea elementelor șirului a.