Acest site foloseşte cookies. Navigând în continuare, vă exprimaţi acordul asupra folosirii cookie-urilor.

Detalii evaluare #58124837

Rezumat problemă

#702 Pascal

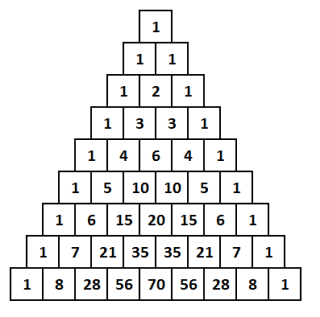Triunghiul lui Pascal este un aranjament geometric de numere ce poartă numele celebrului matematician francez Blaise Pascal (19 iunie 1623 – 19 august 1662), deoarece el a fost prima persoană care a descoperit importanţa tuturor modelelor din componenţa acestuia.

Triunghiul începe cu numărul 1. Acest rând este considerat rândul 0 al triunghiului. Restul numerelor din acest triunghi se formează ca suma celor două numere de deasupra (considerând că toate numerele din afara triunghiului sunt întotdeauna zero). Prin urmare, rândul 1 va fi format din 1 = 0 + 1, 1 = 1 + 0, iar rândul 2 va fi format din 1 = 0 + 1, 2 = 1 + 1, 1 = 1 + 0.

Fie n și p două numere naturale nenule cu proprietățile:

  • p este număr prim;
  • n+1 este o putere naturală a lui p;

Notăm cu M(p) numărul de multipli de p din primele n+1 rânduri ale triunghiului lui Pascal.

Să se scrie un program care citeşte numerele naturale n şi p și determină numărul M(p).

Lot Juniori, Baia Mare, 2013

Rezolvă

Detalii

Problema Pascal Operații I/O pascal.in/pascal.out
Limita timp 0.1 secunde Limita memorie Total: 16 MB / Stivă 16 MB
Id soluție #58124837 Utilizator ilie demian (insertokname)
Fișier pascal.cpp Dimensiune 885 B
Data încărcării 15 Mai 2025, 11:06 Scor / rezultat Eroare de compilare

Evaluare


Mesaj compilare

pascal.cpp:1:1: error: expected unqualified-id before string constant
 "// sursa se utilizeaza faptul ca multiplii de p sunt aranjati sub forma unui fractal\n\n#include <fstream>\n\nusing namespace std;\n\nlong long n,p;\n\n\nlong long putere(long long a,long long b)\n{\n    long long q=1,i;\n    for(i=1;i<=b;i++)\n        q=q*a;\n    return q;\n}\n\nlong long fractal(long long x)\n{\n    long long t=putere(p,x-1);\n    if (x==1) return 0;\n         else return p*(p+1)/2*fractal(x-1)+(p-1)*p/2*t*(t-1)/2;\n\n}\n\nint main()\n{\n    long long k,w;\n    ifstream f(\"pascal.in\");\n    ofstream g(\"pascal.out\");\n    f>>n>>p;\n\n    // determin puterea la care se ridica p ca sa obtinem n+1 (sau log(p,n+1))\n    k=0;w=1;\n    while (w<=n)\n    {\n        w=w*p;\n        k++;\n    }\n\n    // calculez recurent cate 0-uri apar in triunghiul lui pascal scris modulo p\n    g<<fractal(k)<<\"\\n\";\n\n    f.close();\n    g.close();\n\n    return 0;\n}"
 ^

Cum funcționează evaluarea?

www.pbinfo.ro permite evaluarea a două tipuri de probleme:

  • probleme la care rezolvarea presupune scrierea unui program complet
  • probleme la care rezolvarea presupune scrierea unei secvențe de program - câteva instrucțiuni, o listă de declarații, una sau mai multe funcții, etc.

Problema Pascal face parte din prima categorie. Soluția propusă de tine va fi evaluată astfel:

  • Programul sursă este compilat folosind compilatorul corespunzător. Dacă în urma compilării se obțin erori sau avertismente, acestea sunt afișate în această pagină.
  • Dacă programul a fost compilat, executabilul obținut va fi rulat, furnizându-i-se unul sau mai multe seturi de date de intrare, în concordanță cu restricțiile specifice problemei. Pentru fiecare set de date se obține un anumit punctaj, în raport cu corectitudinea soluției tale.

Suma punctajelor acordate pe testele utilizate pentru verificare este 100. Astfel, soluția ta poate obține cel mult 100 de puncte, caz în care se poate considera corectă.