Exerciții
Rezultate 88
Exercițiul #978
Se consideră două tablouri unidimensionale A și B: A=(21,18,14,11,4) , iar B=(46,17,14,8,3). În urma interclasării lor în ordine descrescătoare se obține tabloul cu elementele:
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1061
Variabila x este de tip întreg. Indicați valoarea maximă din intervalul [0,102) pe care o poate avea x, astfel încât expresia C/C++ sqrt(x)==floor(sqrt(x)) să aibă valoarea 1.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1205
Tablourile unidimensionale A și B au valorile A=(18,15,9,5,1) și B=(40,15,13,4,1). Pentru a determina al 5-lea element obținut în urma interclasării tablourilor în ordine crescătoare, se compară elementul cu valoarea xa din A cu elementul cu valoarea xb din B. Indicați valorile lui xa și xb.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1238
Variabilele x și y sunt de tip întreg. Indicați o instrucțiune ce realizează o prelucrare echivalentă următoarea.
x=-abs(y);
| Varianta 1 |
if(x<0) x=-y; else x=y; |
| Varianta 2 |
if(y<0) x=y; else x=-y; |
| Varianta 3 |
while(y>0)
{ x=x*x; y=y-1;} |
| Varianta 4 |
while(y>0)
{ x=x*y; y=y-1;} |
Exercițiul #1273
Șirul lui Fibonacci are termenii 1, 1, 2, 3, 5, 8 ….
În secvența C/C++ de mai jos toate variabilele sunt de tip întreg.
while(x>0)
{ z=y-x;
y=x;
x=z;
}
if(.........)z=1;
else z=0;
Indicați expresia care poate înlocui punctele de suspensie, astfel încât, în urma executării secvenţei obținute, variabila z să aibă valoarea 1 dacă numerele nenule memorate inițial în variabilele x și y (x<y) sunt termeni consecutivi ai șirului lui Fibonacci, sau valoarea 0 altfel.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1693
În secvența de mai jos, toate variabilele sunt întregi. Indicați expresia care poate înlocui punctele de suspensie astfel încât, în urma executării secvenței obținute, variabila p să memoreze valoarea produsului 3!⋅5! (unde s-a notat cu x!, pentru x∈{3,5}, factorialul lui x, calculat ca produs al tuturor numerelor naturale nenule, distincte, mai mici sau egale cu x).
p=1; f=1;
for(i=3;i<=6;i++)
if(i%2==1)
{ f=........;
p=p*f;
} | Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #815
În secvenţa de instrucţiuni de mai jos toate variabilele sunt de tip întreg.
for(i=0;i<5;i++)
{ for(j=0;j<5;j++)
if(...........)
cout<<″1 ″;
else
cout<<″2 ″;
cout<<endl;
}
Indicaţi o expresie care poate înlocui punctele de suspensie astfel încât, în urma executării secvenţei obţinute, să se afişeze pe ecran valorile din figura de mai jos, în această ordine.
1 1 1 1 1 1 2 2 2 1 1 2 2 2 1 1 2 2 2 1 1 1 1 1 1
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1062
În secvența de mai jos toate variabilele sunt de tip întreg și memorează numere naturale.
y=1; x=10; n=8;
while(n>0)
if(n%2==0)
{ x=x*x;
n=.......;
}
else
{ y=y*x;
n=n-1;
}
Indicați expresia care poate înlocui punctele de suspensie astfel încât, în urma executării secvenței obținute, variabila y să memoreze valoarea 108.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1204
Pentru a verifica dacă în tabloul unidimensional (3,7,12,15,17,22,30) există elementul cu valoarea x=6 se aplică metoda căutării binare. Indicați succesiunea de elemente a căror valoare se compară cu x pe parcursul aplicării metodei.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|
Exercițiul #1239
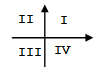
Variabilele reale x și y memorează coordonatele centrului unui cerc, în sistemul de coordonate xOy. Indicați o expresie C/C++ care are valoarea 1 dacă și numai dacă centrul cercului este în cadranul I sau în cadranul al III-lea ale sistemului de coordonate xOy, dar nu și pe axele sistemului.
| Varianta 1 |
|
| Varianta 2 |
|
| Varianta 3 |
|
| Varianta 4 |
|